[논문 리뷰] Handling Missing Data in Decision Trees: A Probabilistic Approach

본 게시글은 개인적인 공부를 위해서 작성된 글이니 비약적인 내용 또는 틀린 내용이 포함되어 있을 수 있습니다

Abstract & Introduction

이 논문은 decision tree 기반의 모델을 활용하여 missing data를 다루는 방법에 방점을 두고 있다.

decision tree는 machine learning model 들 중에서도 가장 각광받는 모델인데, 그 이유는 딥러닝이나 여타 다른 모델에 비해 갖는 장점이 있기 때문이다. 정리하자면,

• Interpretability
• ability to handle heterogeneous (mixed continuous-discrete) data
• ability to handle missing data

결국 딥러닝과 같은 모델에 비해 해석가능하고, 각 columns들이 이질적인 형태를 보이는 데이터나 결측치가 있는 데이터들에 대해서 잘 작동한다는 것이다.

논문에서는 이러한 장점이 있는 decision tree를 활용하여 확률론적인 관점에서 missing data를 해결하는 방법을 제시하고 있다.

이 때, deployment time(배포)과 learning time(학습)에서 각각 확률론적인 방법을 사용해서 missing data를 처리하는 것을 Main Contribution으로 보여주고 있다.

Background

• notation
  • $X$ : RVs 확률변수
  • $x$ : $X$로부터의 관측값
  • $X^o$ : 관측변수
  • $X^m$ : 결측치가 포함된 변수
• Decision Tree
  • 생략
• Decision Forests
  • 생략
• Decision trees for missing data
  • mean, median, mode imputation & PVI(predictive value imputation) : model의 Input으로 들어가기 전에 missing data가 처리되는 방식
    • 데이터 분포에 대한 강력한 가정이 필요함. (때로는 적절하지 못할 수 도 있음)
  • Mulitple imputation with chained equations, surrogate splits(used in CART), MIA(XGBoost) : decision tree에서

Method

1. Expected Predictions of Decision Trees

논문에서는 저자가 제시한 joint distribution $p(\bold{X})$ 를 활용하여 deployment time 에서 missing values를 처리하고 있다. 그리고 기본적으로 기대예측(expected predictions)을 활용하기 때문에 한번에 모든 가능한 imputation된 case를 고려할 수 있게 된다. 그래서 deployment time에서의 기대예측(expected predictions)은 다음과 같이 수식으로 표현할 수 있다.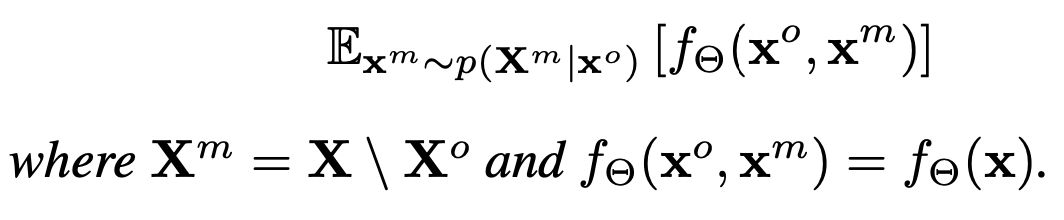

논문은 위와 같은 접근 방식을 활용하여 regression, classification에 적용할 수 있고, 더불어 여타 다른 학습이 완료된 모델들($f_\Theta$)을 활용할 수 도 있다고 이야기하고 있다. 수식에 대해서 살펴보면,

$\bold{x}^m ~ p(\bold{X}^m \mid \bold{x}^o)$ 에 해당하는 부분이 논문에서 제시하고 있는 non-parametic한 분포 추정을 통해 missing values를 처리하는 부분이다. 논문에서는 non-parmetic한 방법으로 추정한 분포로부터의 값을 활용하여 missing values를 imputation을 하고 있는데, Probabilistic Circuits(PCs)라는 방법을 활용하고 있는데, 논문 밖의 내용이라 간단히 설명하면 이렇다. 다른 변수들 $x^o$와 $x^m$를 활용하여non-parametic하게 분포를 추정하고, 이를 적절하게 결합하게 된다.(이때 회로(circuits)처럼 graphical하게 결합된다.논문에서는 이해를 돕기 위해 deep version of classical mixture model이라고 표현하고 있다.) 그림으로 표현하면 다음과 같다.

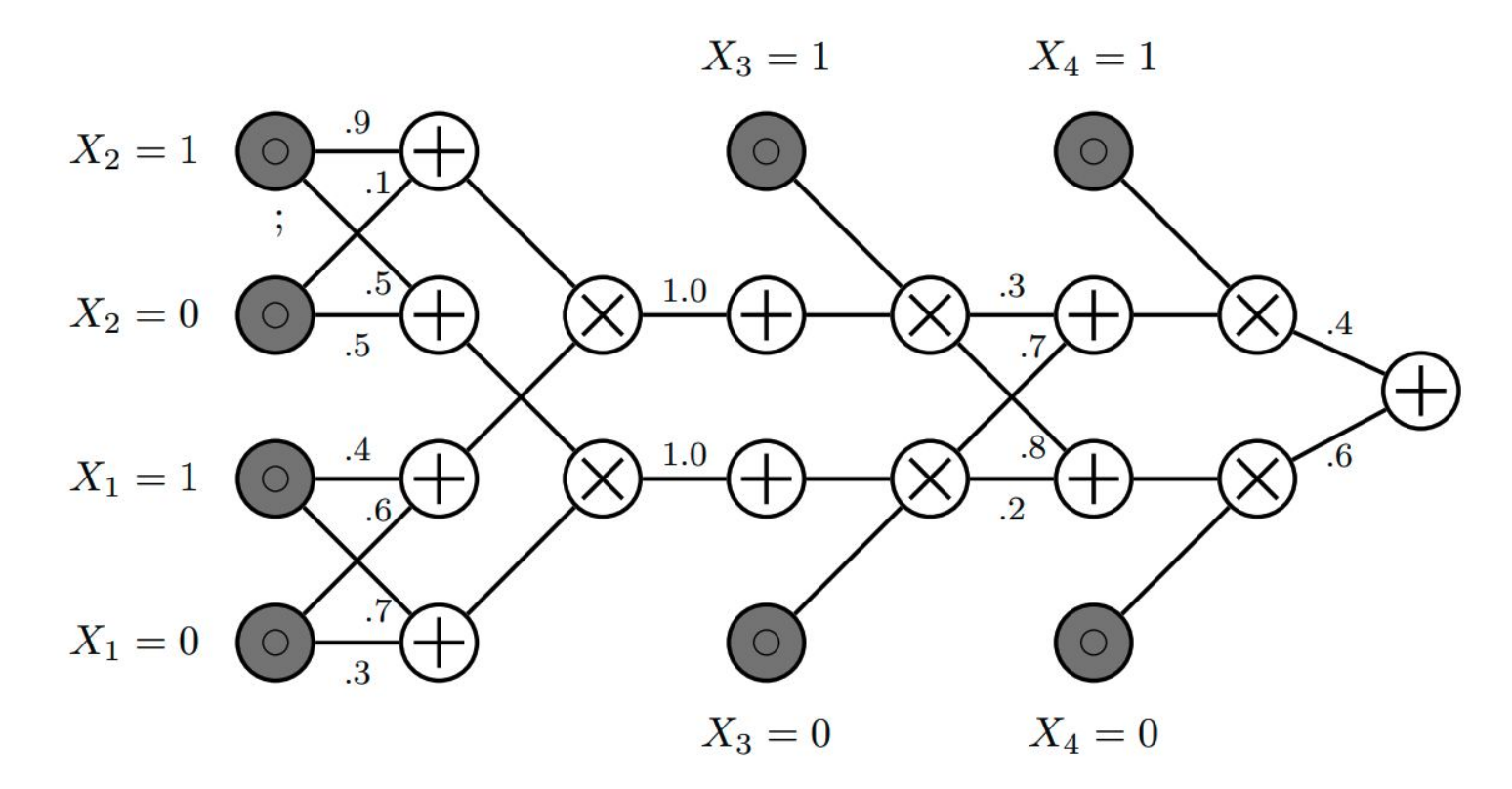
결국, 다른 변수들을 활용하여 non-parametic하게 분포를 추정하고, 이로부터의 값으로 대치하는 것으로 이해할 수 있다.

Missing not at random (MNAR) if neither MCAR nor MAR holds : 관측 변수와 관련이 없는 변수(모르는 변수)와 관련이 있는 missing values 과 같은 case에 대해서는 고려하기는 어려워 보인다… 논문에서도 MNAR에 대한 언급이 없는 것을 보니…

그리고 이러한 방식으로 Imputation을 수행하고, 예측을 수행하게 된다. 그런데 Expectation, 즉 PCs에 의해 서로 다르게 imputation이 적용된 데이터셋에 대한 예측에 기대값을 취하게 된다. 결국 이런 방식을 취하게 되면 서두에서 이야기했듯이, 가능한 모든 imputation case를 고려한 예측을 수행할 수 있게 된다.

이러한 방식은 linear regression, logistic regression 등에서 수행될 수 있는데, Decision trees에서도 적절히 수행될 수 있다.

이를 수식으로 표현하면,

기본적으로 expected prediction을 하기 때문에 논문에서는 tree의 깊이를 비교적 얕게 설정해서 overfitting을 방지하고자 한다.

2. Expected Parmeter Learning of Trees

expectation의 개념이 훈련과정에서도 반복된다. PCs를 통해서 결측치 처리가 완료된 데이터 샘플들에 대해 loss가 계산되고, 그 loss들의 expectation을 최종 Loss로 활용(Expected Loss)하여 최적화를 수행하게 된다. 그리고 이러한 개념으로 학습된 Decision trees의 개념은 여타 다른 ensemble method로 확장될 수 있다. 수식으로 표현하면 다음과 같다.

이 때 최적화에 사용되는 Loss function은 통상적으로 많이 사용되는 MSE를 사용하게 되고, 학습 과정에 L2 regularization이 추가된다.

그리고 이 목적함수에 대한 optimal leaf parameters는 위와 같이 계산이 된다. 결국 PCs에 따라 조금씩 최적의 parameters가 조정이 되는데, 논문에서는 이를 활용하여 기존의 모델을 fine-tuning하여 더 좋은 성과를 보이고 있다.

Experiments

실험은 데이터 셋이 deployment time에 missing values가 존재하는 경우와 learning time에도 missing values가 존재하는 경우로 나뉘어진다. 그리고 데이터에 존재하는 Missing values들은 MCAR(완전히 랜덤하게 존재하는 missing values)라고 가정한다. 논문의 Method에서는 Decision trees로 설명을 했는데, 실제 성과를 측정할 때는 XGBoost를 base line으로 사용하였다.

실험할 때는 RMSE를 활용하여 성과를 측정하였고, missing values의 비율 또한 0.1~0.9까지 다르게 세팅하여 독립적으로 시행하였다.

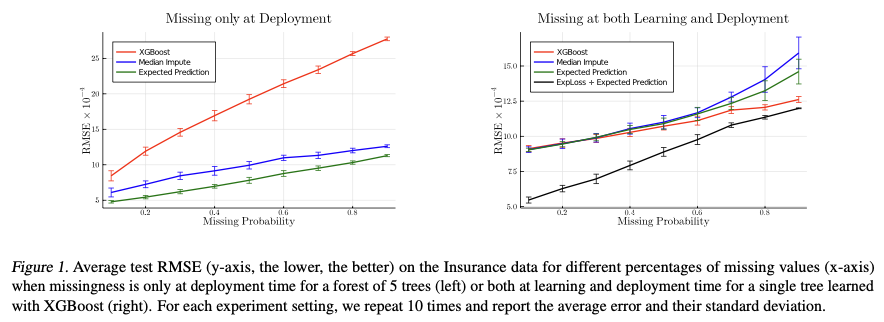
그리고 오른쪽 그림과 같이 Expected Loss로 fine tuning을 진행하고 Expected prediction으로 성과를 측정하였다.

Conclusion

결국 논문의 골자는 PCs(논문 저자들이 다른 논문에서 제시한 technique)을 활용하여 deployment & learning time 각각에서 적용될 수 있는 expected prediction 과 expected loss를 fine tuning을 제시하는 것에 있다.