10 분 소요

본 게시글은 개인적인 공부를 위해서 작성된 글이니 비약적인 내용 또는 틀린 내용이 포함되어 있을 수 있습니다

Abstract & Introduction

Abstract

본 논문에서는 missing values가 있는 데이터셋에 대해서 머신러닝 모델을 적용할 때, 발생하는 Fairness concerns에 대해서 다루고 있다. 공정성에 개입하여 학습시키는 모델들이 여러 가지 제안되어 왔는데(MIP 모델 등 뒤에서 설명) , 이러한 모델들은 보통 완전한 학습 datasets을 가정하고 있다. 따라서 missing values가 있는 불완전한 datasets들에 대해 imputation(결측값 대치)를 한 뒤 공정성에 개입하는 머신러닝 방법들이 적용된다면, 불공정한 모델이 만들어질 수도 있다.

여기서 Fairness라는 표현이 모호한데, 공정성이라고 해석하지만 모델이 얼마만큼 편향되었는지를 이야기하는 것이라고 생각하면 좋다. 또, 모델이 편향되었다는 의미는 대표적인 한 기업의 사례로 설명할 수 있다.

  • Example case : Northpointe사가 만든 재범 확률을 예측하는 알고리즘 COMPAS가 이를 이해하기 쉬운 예시이다. COMPAS 알고리즘은 피고인의 일반범죄와 강력범죄 각각에 대한 재범률을 측정하여 피고인에 대한 risk score(1~10)를 판사에게 제공한다. 그리고 판사는 이를 보조자료의 형태로써 활용하여 형량을 선고 및 가석방에 대한 도움을 받을 수 있다. 그런데 2016년 이 알고리즘이 인종편향적인 결과를 보여준다는 통계가 나오게 된다. 백인의 경우 risk score가 1에 가장 많이 분포하고 10까지의 비율이 점차 감소하는 반면, 흑인의 경우 risk score가 1~10까지 고루 분포한다. ‘여기까지만 들었을 때는 그럴 수도 있지 않겠느냐’라는 생각이지만 조금 더 설명을 이어 가보겠다. 당시 재범률이 높은 것으로 예측되었지만 실제로 2년간 범죄를 저지르지 않은 것으로 드러난 경우가 흑인은 45%, 백인은 23%로 두배에 달하였다. 그리고 재범률이 낮은 것으로 예측되었지만 실제로 2년간 범죄를 저지른 경우가 백인이 48%, 흑인이 28%였다. 각각, 약 두배에 달하는 차이이고, 이는 모델이 정확성을 떠나서 공정하지 못하고 인종편향적이라고 이야기 할 수 있다.

그래서 논문에서는 결측값이 포함된 상태에서 학습이 가능한 decision tree 기반의 모델을 제시하고 있다. abtract이기 때문에 간단하게만 설명하면, 결측치가 포함되어 있는 속성으로 decision tree를 하되 fairness-regularized objective function으로 최적화 과정을 수행한다.

마지막으로 논문에서는 제시하는 방법을 통해 imputed dataset에 fairness intervention method (model)를 적용하는 것보다 더 좋은 성능을 보이고 있다.

Introduction

abstract에서 이야기하였지만, 논문이 가장 중요하게 쳐다보고 있는 곳은 “missing values”와 “fairness”이다. missing values는 모델 학습과 관련해서 유의미한 영향을 미치는 경우가 있을 수 있다. 이렇게 missing values가 발생하는 경우는 여러가지가 있다. 랜덤하게 발생하는 경우가 대부분이지만 인간과 관련된 데이터의 경우 사회인구학적인 특성(인종, 소득, 나이)과 연관되어 발생하는 경우도 있다. 예를 들면, 저소득 환자가 비용이 많이 드는 의료검사를 거부해서 결측값이 생기는 경우가 있다. 또, 글씨 pont의 크기가 너무 작아서 나이가 많은 사람들이 설문에 응답하지 못했거나, Non-native speakers에게 너무 어려운 언어로 설문이 되어 있어서 발생하는 결측값이 있을 수 도 있다.

이러한 경우, 상식적으로 어떤 값을 임의로 대치해서 모델 학습 (training model) 또는 데이터 분석(data analysis)을 수행하는 것은 적절하지 않아보인다 !

머신러닝의 기본적인 pipline을 생각해보자. 데이터가 모델로 들어가기 전에 먼저 전처리 단계를 거치게 된다. 그리고 전처리 단계 내에는 우리가 다루고자 하는 missing values들을 다른 값으로 대치(performing imputation)하거나 삭제(dropping missing values) 하는 단계가 있다. 하지만, 앞서 이야기했듯이, 이러한 전처리 방식은 모델의 성능을 떠나서 편향된(biased) 모델, 즉 공정하지 못한 모델이 만들어질 수 있다.

‘자주 사용되는 mean imputation, median imputation은 각 attriubtes가 평균 또는 중위값 근처 있다’라는 데이터 분포에 대한 강력한 가정을 하고 있다.

본질적으로, 이렇게 편향된 결과가 나올 수 있는 우려가 있는 데이터를 가지고 앞서 잠깐 언급한 Fairness한 머신러닝 모델들을 적용한다면, 어떻게 될까?

논문에서는 이러한 문제에 해결하기 위해서 missing values 처리와 fairness한 머신러닝 모델들을 연결하여 해결책을 제시하고 있다. 이 때, missing values의 처리 방식이 fairness에 어떠한 영향을 미치는지 이론적으로 분석하고 있다.

missing values를 임의의 값으로 대치함으로써 발생하는 잠재적인 discrimination risk에 대한 이론적인 분석은 다음과 같은 세 가지 요인을 중점으로 살펴보게 된다.

discrimination risk라는 용어가 등장하는데 논문에서는 Fairness한 정도를 측정하는 지표정도로 보면 될 듯 하다.

  1. imputation method의 성능이 각 group attributes마다 다르게 나타날 수 있다. 그 결과 imputed data는 모델의 bias에 영향(Inherit and propogate)을 미치게 된다. ( 직관적으로 이해하자면 imputation method로 인해 남성:0, 여성:1 일 때의 정확도(또는 FPR,FNR)의 차이가 크게 벌어진다는 뜻이다.)
  2. imputation method을 활용하여 훈련 과정에서 fairness하게, 즉 unbiased하게 학습되었다고 해도, 다른 Imputation 방법이 적용된 새로운 test data에 대해서는 그렇지 못할 수 도 있게 된다.
  3. 마지막으로 보편적으로 downstream에 적용될 수 있는 fairness한 모델 적절한 imputation method는 없다.

위의 세 가지를 이론적 분석을 통해, 이를 극복하고자 하는 Imputation을 하지 않는, Fair MIP Forest라는 방법을 제시한다.

Introduction이니 이 방법에 대해 큰 틀에 대해서 잠깐만 언급하면,

  • Missing values를 다루기 위한 MIA( missing incorporated as attribute) 방법
  • fairness를 규제하기 위한 목적 함수를 최적화하는 방법인 MIP(mixed integer programming)

이 두 가지를 결합한 decision tree 모델이다. 이 두 가지 방식을 결합하기에 fairness와 accuracy를 동시에 최적화하여 이 두가지 지표의 trade-off 측면에서 좋은 성능을 보여주게 된다.

missing values를 다루는 방식에 대한 논문이다 보니 related works에서 이를 다루는 방식에 대해 개괄적으로 살펴 볼 필요가 있다.

대표적인 방법으로는

  • 단일 대치법 (Single Imputation) : Inserting dummy values, mean-imputation, regression imputation( k-nearest neighbor regression). 더미 값이나 평균 값 또는 회귀적인 방법에 의한 값 하나로 대치.
  • 다중 대치법 (Multiple imputation) : Imputation method that draws a set of possible values to fill in missing values, as opposed to single imputation that substtitutes a missing entry with a single value. 단일 대치법을 여러 번 적용한 뒤 결과값을 추합하는 방식. (Ensemble 방법에서 일반적으로 사용된다.)
  • 행 삭제 (Dropping rows with missing entries)

이 있다. (논문에서 소개하는 Fair MIP Forest 방법은 서로 다른 랜덤 미니 배치가 각각의 트리로 훈련되는데, 이 때 각각은 다르게 결측치를 처리하기 때문에 다중대치법(Multiple imputation)에 해당한다.)

더불어, 논문의 목적은 missing values를 decision trees 기반의 모델로 처리하게 된다. 그래서 decision trees 기반의 missing values 처리 방식에 대해 간단하게 살펴보자.

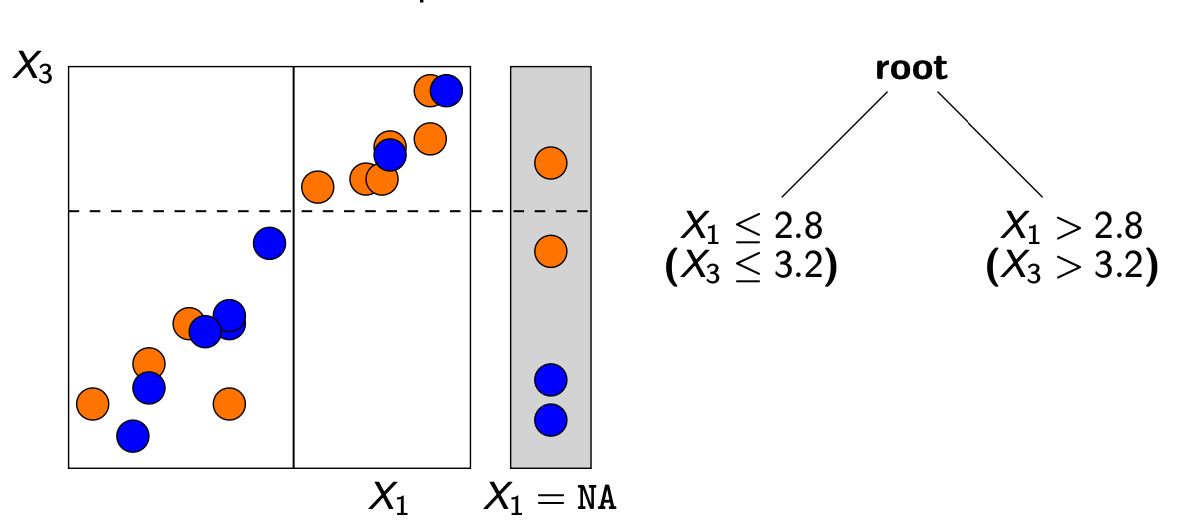
  • surrogate splits : 관련이 있는 attributes를 활용하여 missing values를 분리한다surrogate_splits

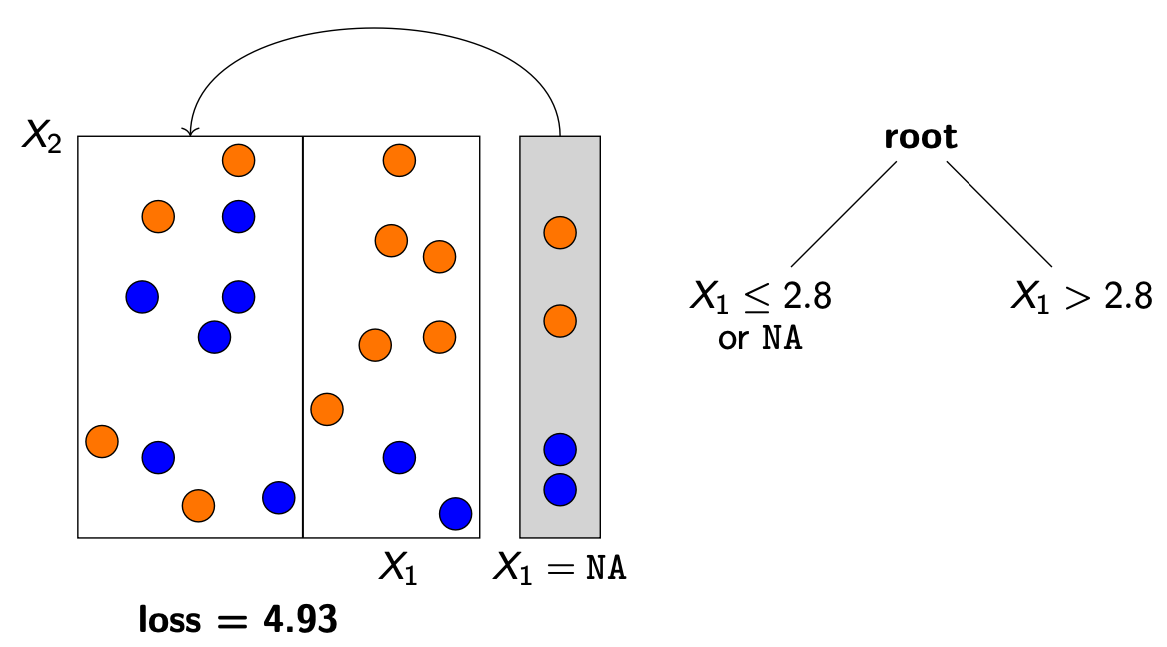
  • block propogation : loss가 최소가 되는 노드 방향으로 missing values를 보내게 된다.block_propogation

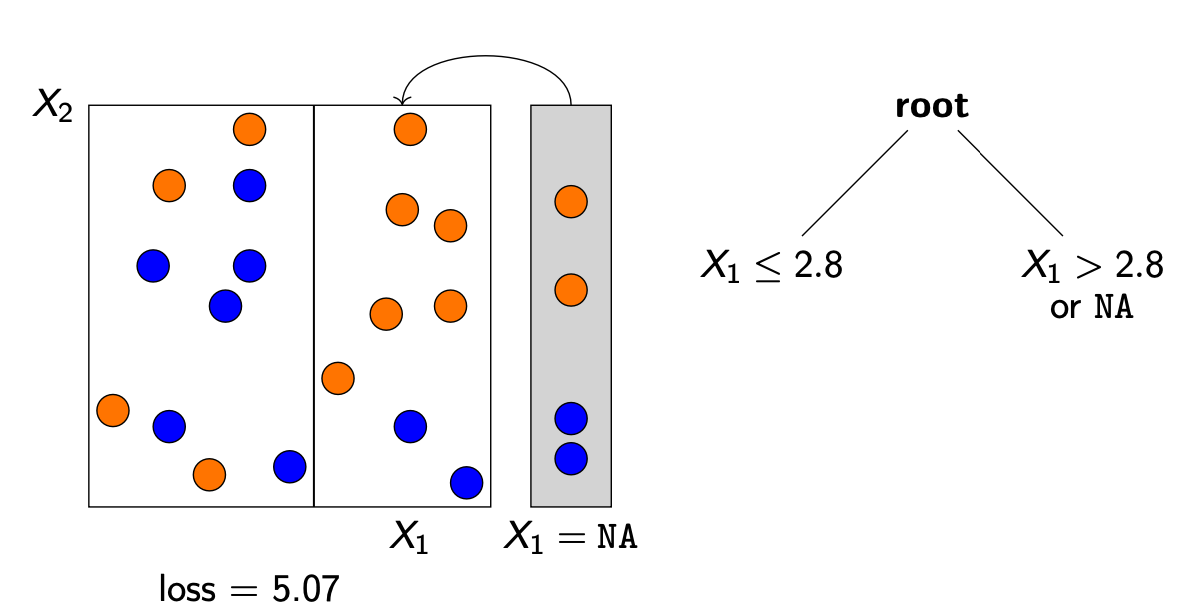
    block_propogation2

  • missing incorporated as attribute (MIA) : 특정 Threshold와 feature에 대해 3가지 경우의 Loss를 고려해서 missing values가 특정한 노드로 보내지도록 한다.

    MIA

Framework

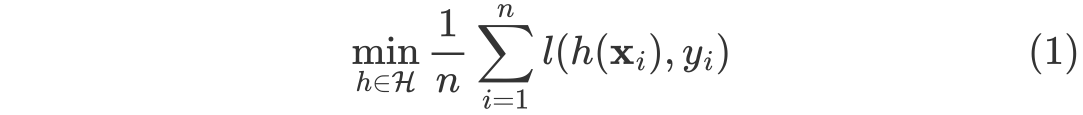
  • Supervised learning and disparate impactimage-20230312130413832

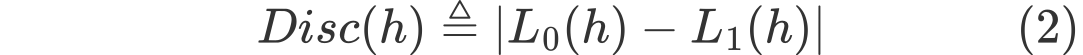
image-20230312130441554

(1) 은 특정 모델 h에 대한 predicted output과 true output간의 loss를 계산한 부분이다. loss 에 해당하는 부분은 task에 따라 조금 씩 달라질 수 있다.(ex mean squred error)

(2)에 해당하는 식은 모델이 얼마 해당 모델이 group s에 따른 결과가 얼마나 차별적인 결과를 나타내는지를 보여주는 Discrimination risk이다. ((3)의 수식을 참고)

image-20230312130357221

Disc(h)에 대해서 조금 더 직관적으로 설명해보면, 모델의 Loss가 성별이 0(여자)일 때와 성별이 1(남자)일 때의 차이가 크다면 discrimination risk는 커지게 되는 것이다. (1)과 (2)를 조합하여 다음과 같은 식을 만들게 되면, 모델의 biased를 고려한 일반적인 fairness intervention method가 된다.

image-20230312130349640

  • Data missingness

    image-20230312130341243

실제 데이터의 구성에 관한 notation은 위와 같다. 결측치가 없는 관측 변수 $X_{obs}$와 missing values가 포함된 $\tilde{X}_{ms}$ 변수로 이루어져 있다. missing values가 포함된 변수에서 missing values가 있는지 없는지 판단하기 위해 binary variables가 도입된다. binary variables $M=0$라면 missing values가 없는 것이고, 반대로 M = 1이라면 missing values가 있다는 의미이다.

  • Type of missing values
    • Missing completely at random(MCAR) if M is independent of $X$ : 관측 변수와 무관한 missing values
    • Missing completely at random (MAR) if M depends only on the obsereved variables $X_{obs}$ : 관측 변수들과 관련이 있는 missing values
    • Missing not at random (MNAR) if neither MCAR nor MAR holds : 관측 변수와 관련이 없는 변수(모르는 변수)와 관련이 있는 missing values

real-world에서는 대부분의 missing values가 MNAR를 따르고 있지만 이론적인 연구를 위해 위와 같은 세 가지 type으로 missing values이 가질 수 있는 data distribution 구분하고 있다.

  • Data Imputation

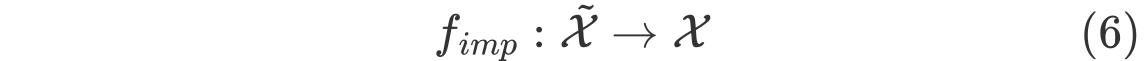
    image-20230312130331830

miss values가 포함된 feature vector에 $\tilde{X}$에 대해서 missing values를 다른 값을 대치하는 mapping function을 위와 같이 표시한다.

Risks of Training with Imputed Data

본격적으로 이론적 분석을 통해 Introduction부분에서 이야기했던 imputed data가 가질 수 있는 세 가지 문제에 대해 주목한다.

Biased Imputation method

첫번째는 Imputation method가 group attributes에 따라 어떻게 차별적인 performance를 보이는지에 관한 부분이다.

그래서 imputation method에 관한 performance는 다음과 같이 표시할 수 있다.

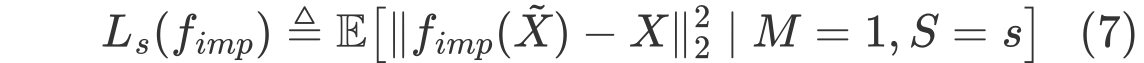
image-20230312130320668

위 수식은 group attribute $S$의 특정한 값이 $s$일 때 (ex. Race = 1) 결측값에 imputation을 한 $f_{imp}(\tilde{X})$와 실제 데이터 $X$간의 차이를 2norm의 제곱을 한 형태이다. (실제 데이터 $X$가 주어지는데 이는 이론적인 분석을 위한 가정인 것 같다.)

그리고 Dicrimination risk는 다음과 같이 정의할 수 있다.

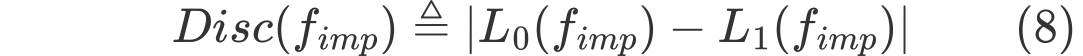
image-20230312130314328

위와 같이 수식을 사용하면 Group attribute에 따른 performance를 구할 수 있게 되고, 이 차이를 통해서 얼마나 한 그룹으로 biased 되어 있는지를 계산할 수 있게 된다.

  • Theorem 1

    가정을 최대한 단순화하여 각각의 그룹들은 MCAR(완전 랜덤하게 missing values가 존재)이고 관측변수가 없다고 가정하면

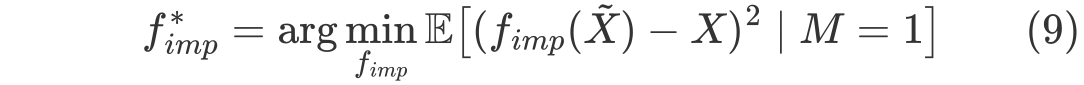
    image-20230312130305569

    로 표현할 수 있고, Discrimination risk는 다음과 같이 표현할 수 있고 이를 분해하면 다음과 같은 식을 얻을 수 있다.

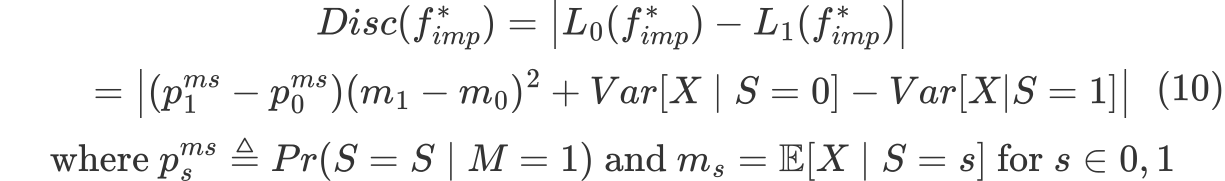
    image-20230312130258813

    그리고 분해된 식으로부터 data imputation이 유발할 수 있는 discrimination 세 가지 얻을 수 있다.

    • 두 그룹간의 missing values의 비율 차이
    • 두 그룹간의 평균의 차이
    • 두 그룹간의 분산의 차이

    결국 이 세 가지에 의해 그룹 간에 missing values의 비율 차이, 평균 또는 분산이 크게되면 결국 Discrimination risk는 커지게 되고 imputation에 의해 biased한 모델이 되게 된다.

    결국 imputation method를 고려할 때는, 위와 같은 세 가지 factor들을 적절히 고려하여 조정하는 절차가 필요해질 수 있다.

Mismatched Imputation Methods

두번째 이론은 training time에서 적절한 Imputation이 적용되었다고 할지라도 testing time에서 test data에 적용되는 Imputation이 다른 Imputation이 적용되면 결국 discrimination risk가 증가된다는 것이다.

여기서 한 가지 testing time에서 똑같은 training time과 동일한 imputation을 적용하면 되는 것 아닌가 하는 생각을 해볼 수 있다. 그런데 논문에서 실제로는 개인 정보 보호 문제로 인해 imputation 방법이 사용자에게 공개되지 않을 때도 있다고 이야기하고 있다.

다음은 training time과 testing time에서 사용되는 Imputation method가 다를 때 발생하는 문제를 수식으로 정리한 내용이다.

  • Thorem 2

    먼저 특정 group attribute $s$에 대해 imputation이 적용된 Predictive model $h$의 성능에 관한 수식은 다음과 같이 표현된다.

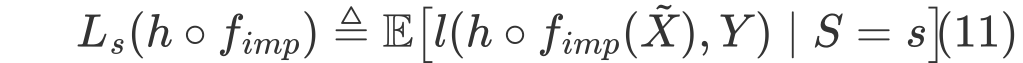
    image-20230312130242691

    그리고 group attributes s 가 0 또는 1 이면서 MCAR 이라고 가정하면

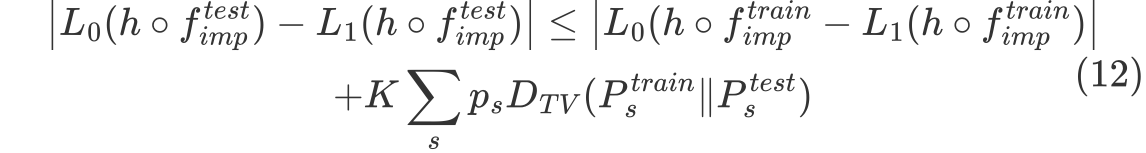
    image-20230312130232752

    • 앞 쪽의 식은 imputation이 적용된 test data가 사용된 모델의 discrimination risk

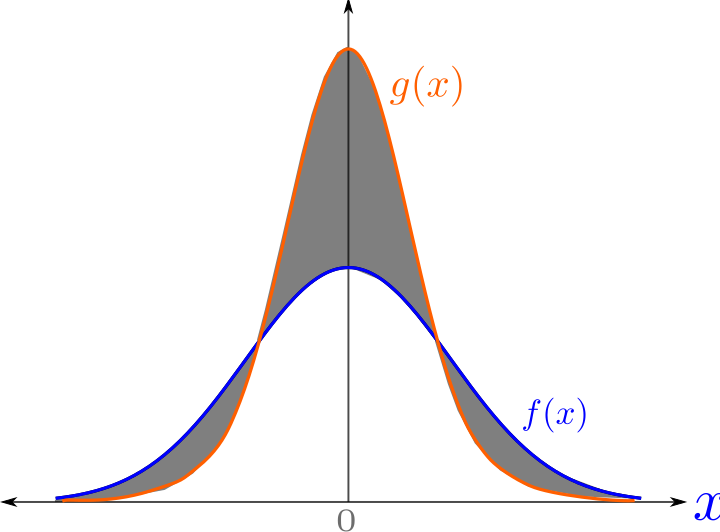
    • 뒤 쪽의 식은 imputation이 적용된 train data가 사용된 모델의 discrimination risk과 train data와 test data의 total variation distance의 총합에 해당한다. TV는 train data의 확률 분포와 test data의 확률 분포 간의 거리의 총합, 즉 두 분포의 차이의 절대값의 총합에 해당한다.

    • 그리고 결국 training time과 testing time에서 서로 다른 imputation이 적용되면, 두 데이터 간의 확률 분포 차이의 절대값에 총합만큼 잠재적인 loss가 발생한다.

    • Total Variation distance 예시 이미지

      Total_variation_distance.svg

Imputation Without Being Aware of the Downstream Tasks

마지막 Theorem은 어떤 머신러닝 Model을 적용하더라도 missing values가 존재하게 되면, Fairness와 Accuracy 측면에서 잘 작동하는 fairness intervention method가 존재하기 힘들다는 것이다.

(1) 식에서 표현한대로, fairness intervention methods는 다음과 같이 나타낼 수 있다.

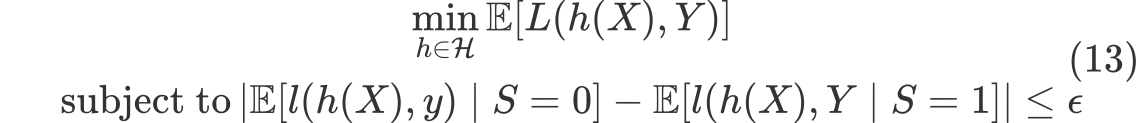
image-20230312130006413

그러나 Imputed data에 대한 fairness inetervention methods는 다음과 같다.

image-20230312130036112

(13)의 식을 따르는 predictive models $\mathcalc{H}$는 존재할 수 있다. 그러나 missing values가 존재하는 상황에서 데이터 셋과 missing values의 특징에 따라 imputation을 다르게 적용해야 한다. 더불어, 예측 모델 자체가 Imputation 방법에 의존적인 상황에서, 이 들을 모두 만족하는 predictive models $\mathcalc{H}$가 존재하기 힘들다는 것이다. 결국 (14) 식처럼 식의 조건을 만족시키기란 쉽지 않다는 이야기이다. 사실 이에 대한 example case를 설명해주고 있는데 잘 이해하지 못하였다.)

Fair Decision Tree with Missing Values

앞서 이론적으로 imputation method 자체의 한계를 살펴보았다. 논문에서는 그래서 imputation process를 거치지 않기 위해 missing incorpoarted in attribute 와 mixed integer programming을 결합한 decision tree 기반의 모델을 제시한다.

Fair MIP Forest Algorithm

앞서 설명한 두 가지 방법의 background는 다음과 같다.

  • Missing Incorporated in Attribute (MIA)

MIA란 결측값을 의사결정나무에서 특정한 방식인데, 다음과 같은 세 가지 경우를 고려해서 오류가 최소가 되는 방향으로 결측값을 노드로 향하게 한다.

MIA

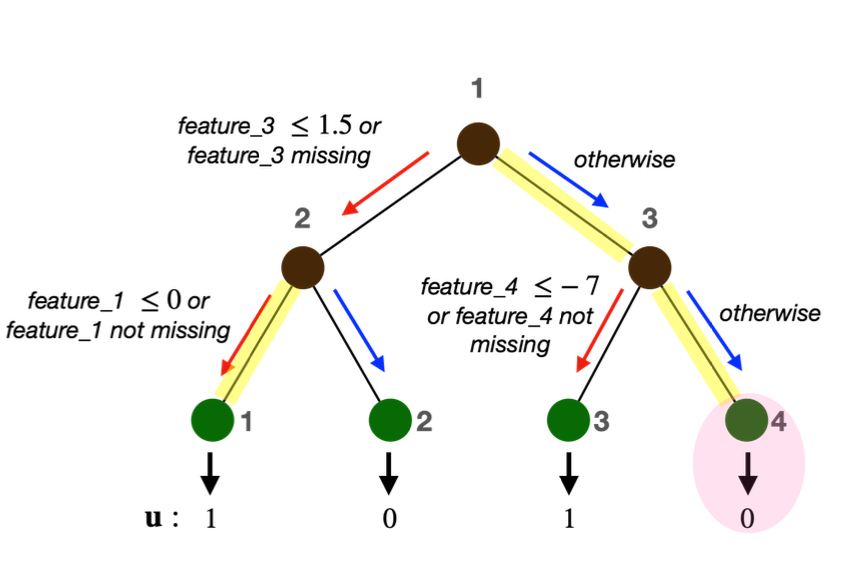
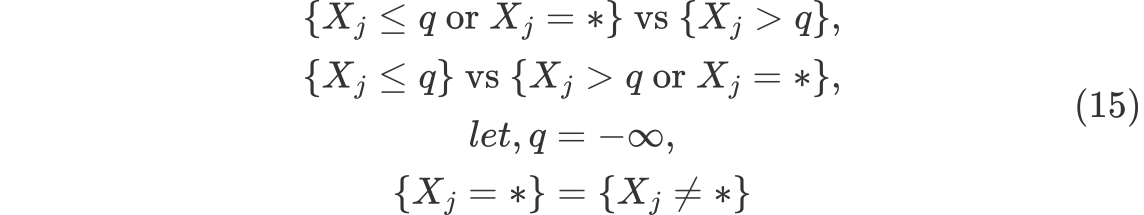
image-20230313020407259

  • Mixed integer programming (MIP)

    image-20230313020423085

image-20230313020455560

기본적으로 missing values가 있는 data에 대한 Decison tree는 위와 같이 표현할 수 있고, 여러 개의 binary(integer) variables와 continous variables(threshold)가 등장한다. (여러 개의 binary variables가 등장하는 이유는 Mixed integer programming을 풀 때, binary variables가 부등식 제약조건으로 포함되기 때문이다.

image-20230313020513791

더불어, 예측 모델을 표현하기 위해 $w_i$ 와 $z_i$ 변수를 추가되는데 핵심적인 binary variables로 보여진다.

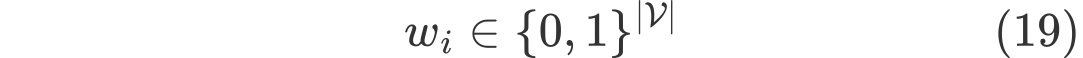
image-20230313020532448

$w_i$는 데이터 포인트가 각 branch node에서 어떤 방향으로 움직일지를 나타내는 값으로 1일 경우, 왼쪽 branch 로 이동하게 된다. (반대는 0으로 이동)

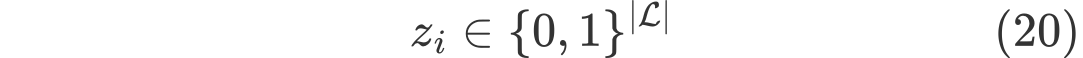
image-20230313020543207

$z_i$는 데이터 포인트가 도달할 leaf node를 나타내고 $z_{i,l}=1$일 경우 데이터 포인가 leaf node $l$에 도달하게 되고, 이 때의 예측값은 $u_l$이 된다. 결국 골자는 이 두 가지에 제약을 걸어둠으로써 Fairness를 유지하도록 하는 것에 있다.

MIP1MIP2

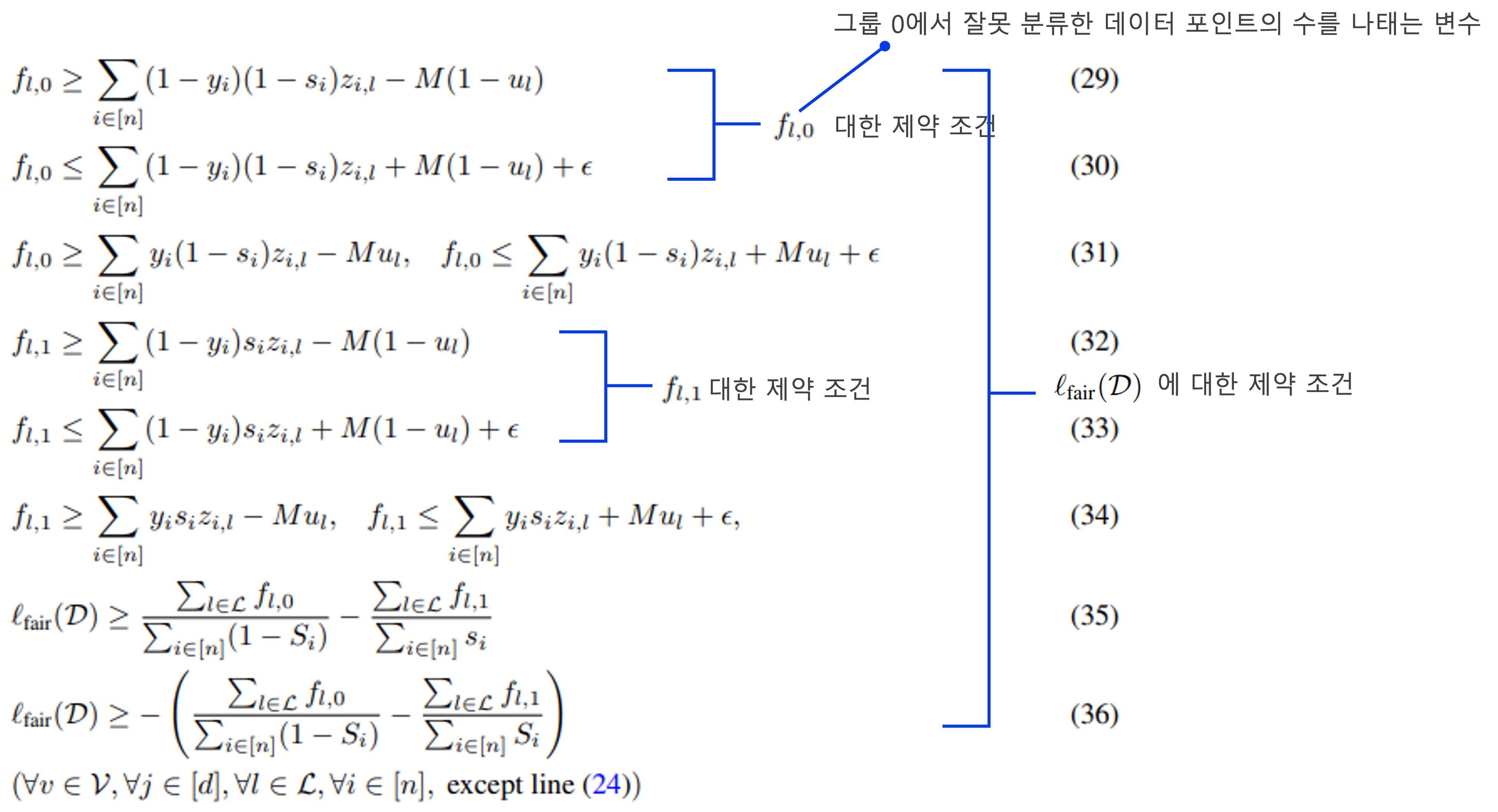
식을 간략하게 요약하면, mixed integer programming (혼합정수계획법)을 사용하여 decision tree를 학습시키는데, user loss function에 Fairness regularizer( Statistical parity, Equalized oods, Accuracy parity )를 더한 loss function을 최적화 시키게 된다. MIP는 보다시피 많은 Integer형태의 부등식 제약 조건들이 많이 포함되어 있다. 그래서 이러한 MIP(혼합정수계획법)을 푸는 것은 computational cost가 굉장히 높다.

  • Fair MIP Forest

그러나 우리가 학습시키는 ensemble method는 각각의 tree에 대한 optimum을 찾는 부담을 갖지 않아도 된다. 왜냐하면 약한 분류기를 여러 개 만든 뒤, 합치는 bagging 방법을 사용하면 되기 때문이다.

Experimental Results

  • Dataset
    • COMPAS, Adult, high school longitudinal study(HSLS)
    • COMPAS, Adult dataset의 경우 원래 missing values가 없기 때문에 다음과 같은 비율로 missing values를 생성함.
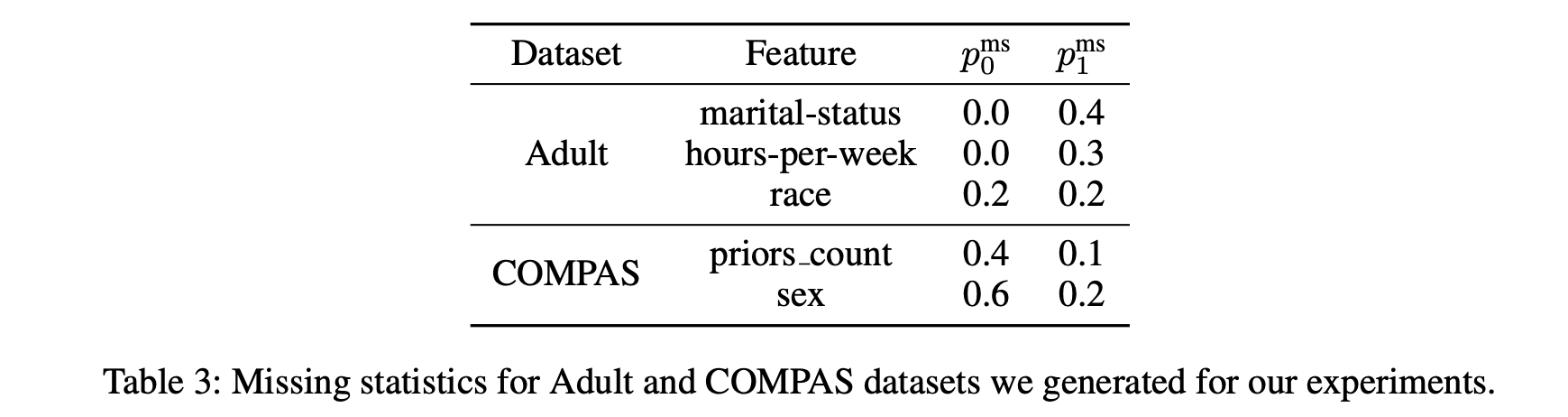
    • ms_values
    • Adult dataset는 성별(0 : 여성, 1 : 남성) 을 sensitive attribute로 사용함
    • COMPAS dataset는 인종(0 : 흑인, 1 : 백인) 을 sensitive attribute로 사용함.
    • HSLS dataset은 어떤 특정 group attribute에 따라 missing values가 있는 것이 아닌, 불규칙적으로 missing values의 pattern들을 가짐.
    • 다음은 HSLS의 data description이다.
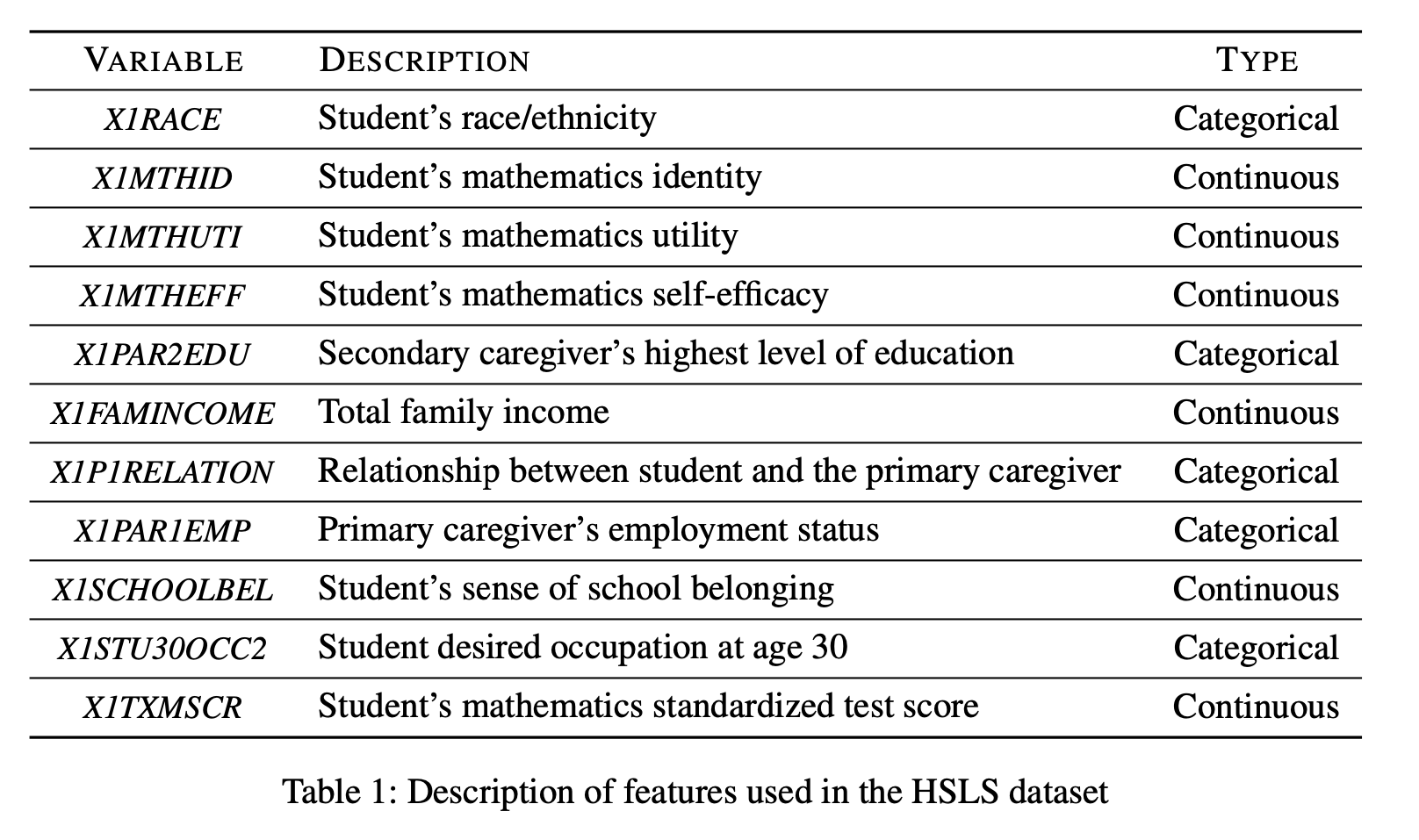
    • data_decription

  • Setup

    • Hyperparmeters
      • tree depths : 3
      • Model의 computational cos가 높기 때문에 tree의 깊이와 training time을 60초로 설정하는 등의 규제를 사용하였음.
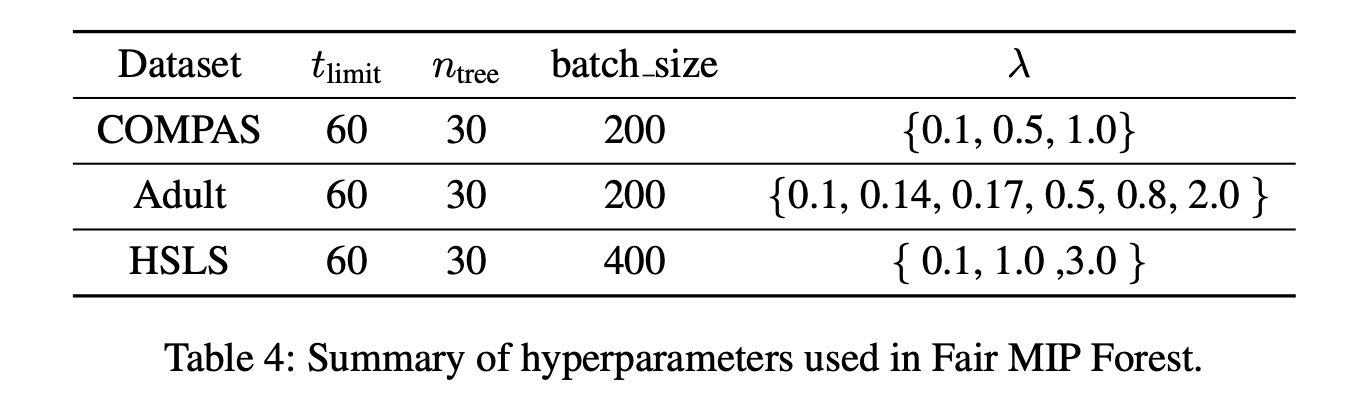
      • hyperparameters

    • Comparison model

      • mean imputation method based forest
      • knn imputation method based forest

      논문에서는 아래의 Fairness ML을 비교 모델로 삼고 있는데, 첫번째 저자의 이름을 따서 부름.

      • exponentiated gradient algorithm(Agarwal)
      • disparate mistreatment algorithm(Zafar)
      • equalized oods algorithm(Hardt)

  • Fairness regularization

    • COMPAS, HSLS dataset는 FPR의 차이가 거의 없어서 FNR의 차이를 규제함.
    • 반대로 Adult dataset에서는 FNR 차이가 무시해도 될 정도여서 FPR의 차이만을 규제함.
  • Discussion

COMPAS dataset의 경우 기존의 fairness ML에 imputation method를 적용했을 때보다, Accuracy-FNR Difference 측면에서 FairMIPForest가 가장 좋은 결과를 보임.

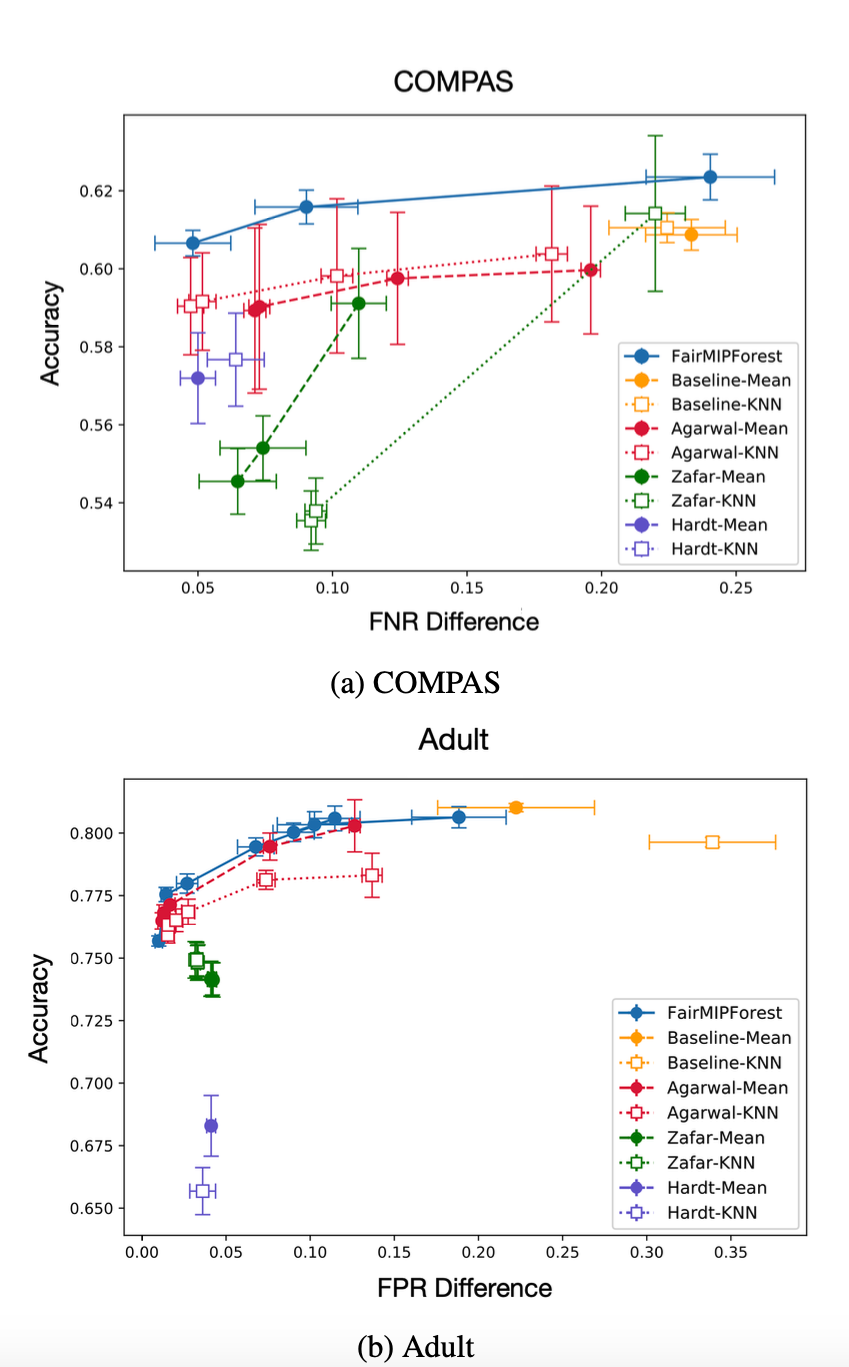
Reesult

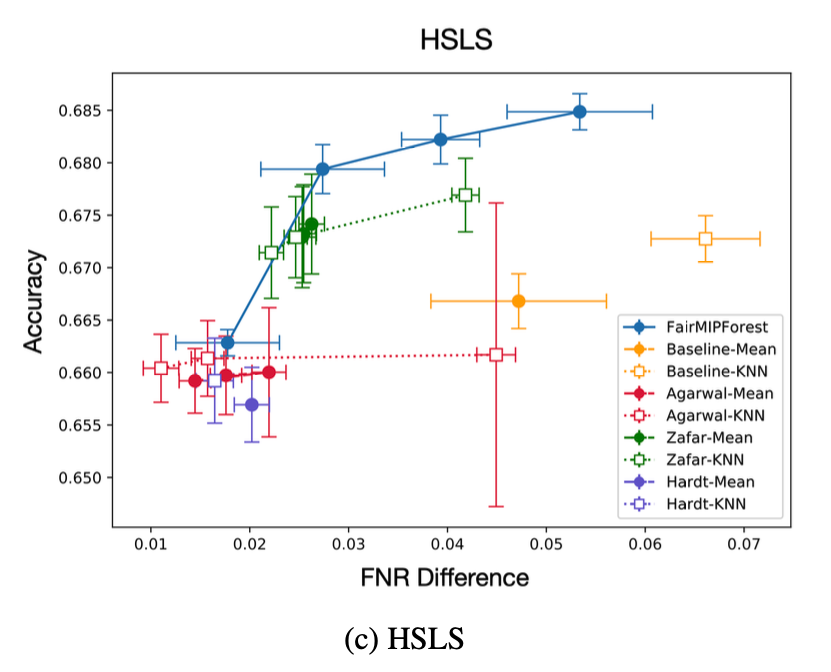
result2

일반적으로 Accuracy와FNR Difference 측면에서 FairMIPForest가 좋은 성과를 보였고, 다른 Fairness ML의 경우 dataset과 imputation method에 따라 일관되지 못한 성과를 보이고 있다.

Future Work

  • Desining fair imputation methods
  • Decision tree 기반의 모델 외에 imputation 방법을 사용하지 않는 other ML models
  • Other fairness metrics

등 과 관련한 연구들이 더 필요할 것으로 생각된다.

댓글남기기

참고

python code

3 분 소요

무심코 파이썬 코드를 작성해서 파이썬답지 못했던 코드들을 떠올리면서… 파이썬 클린코드라는 책을 읽고 재구성하였다.

BYOL

3 분 소요

본 게시글은 개인적인 공부를 위해서 작성된 글이니 비약적인 내용 또는 틀린 내용이 포함되어 있을 수 있습니다

SimCLR

6 분 소요

본 게시글은 개인적인 공부를 위해서 작성된 글이니 비약적인 내용 또는 틀린 내용이 포함되어 있을 수 있습니다