Gaussian Kernel Density Estimation
본 게시글은 개인적인 공부를 위해서 작성된 글이니 비약적인 내용 또는 틀린 내용이 포함되어 있을 수 있습니다
밀도추정(Density Estimation)
우선, 데이터란 어떤 변수가 가질 수 있는 다양한 가능성 중의 하나가 실현된 것이라고 볼 수 있다. 즉, 데이터는 어떤 분포를 따르는 랜덤박스에서 나온 하나의 값이라고 생각해볼 수 있다. 그리고 밀도추정이란 여기서 “어떤 분포”에 해당하는 부분을 추정하는 것이다.
다시 말해, 관측된 데이터(확률 표본)들의 분포로부터 데이터의 본질적인 특성인 모수의 확률 분포를 추정하고자 하는 것이 밀도 추정(Density Estimation) 이다.
데이터가 충분히 많다면, 데이터들의 분포를 통해 모수의 확률 분포를 가늠해볼 수 있다. 그리고 어떤 변수가 분포를 통해 어떤 값을 가질 수 있는지에 대한 가능성의 정도를 추정할 수 있게 된다.
- 확률밀도함수(Probability Density Function)
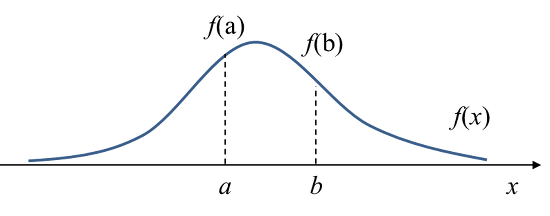
어떤 $x$변수(random variable)에 대해서 밀도를 추정한다는 것은, $x$에 대한 확률 밀도 함수를 추정한다는 의미와 같다. 어떤 변수 $x$에 대해서 확률밀도함수 $f(x)$가 위와 같다고 하자.
이 때, $f(a)$는 $x = a$에서의 확률 밀도, 즉 변수 $x$가 $a$라는 값을 가질 상대적인 가능성을 의미한다.
여기서 유의해야 할 것은 확률이다. $x=a$일 때의 확률은 $0$이다. $f(a)=0$이 아니라는 말이다. 확률은 특정 구간 $a$, $b$사이의 확률밀도함수의 적분값으로 계산된다. $P(a≤x≤b)= \int_a^bf(x)dx$이다.
결론적으로, 확률밀도함수를 구할 수 있다면, 그 변수가 가질 수 있는 값의 범위 및 확률분포, 전반적인 변수의 특성 모두를 알 수 있다. 따라서, 밀도추정은 통계,기계학습, 파라미터 추정 등에서 굉장히 중요하다.
이렇게 중요한 밀도를 그렇다면 어떻게 추정할 수 있을까?
Parametric & Non-parametric Density Estimation
밀도 추정은 크게 Parametric한 방법과 Non-parametric한 방법 두가지로 나뉜다.
- parametric한 방법은 데이터의 모수가 어떠한 분포를 따른다고 정하는 방법이다. 예를 들면 변수 $x$의 모수는 정규분포를 따른다고 정해버리는 것이다. 이렇게 되면, 그저 데이터 샘플들에 대한 평균과 분포만 구하면 되는 간단한 문제가 된다. 그러나 이러한 방법은 이야기만 들어도, 굉장히 현실적이지 못한 가정이다.
- Non-parametric한 방법은 데이터들의 샘플들을 바탕으로 확률밀도함수를 추정하는 방식이다. 간단한 예는, 히스토그램(histogram)이 있다.
앞서 언급한 히스토그램은 불연속적이고, x축의 값(bin)을 어떻게 설정하느냐에 따라 히스토그램이 달라진다. 뿐만 아니라 연산의 문제 때문에 고차원 데이터(high dimensional data)에 적용하기 어려운 측면이 있다.
따라서 이러한 문제점 때문에 Kernel Density Estimation이라는 방법이 많이 사용된다. 이 방법은 이름 그대로 Kernel function(커널 함수)를 활용해서 Density Estimation을 하는 방법이다.
- Kernel function이란 원점을 중심으로 대칭이면서 적분값이 1인 non-negative인 함수로 정의된다.
- $\int_{-\infty}^{\infty}K(u)du=1$
- $K(u)=K(-u), K(u)\geq0,$ ∀$u$
Kernel Density Estimation & Gaussian KDE
Kernel Density Estimation을 수식으로 표현하면, 다음과 같다.
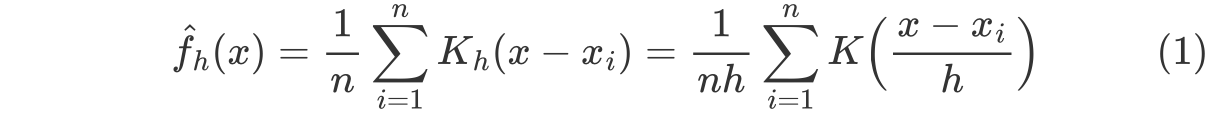
$x$는 random variable이고, $x_i$는 샘플 데이터이다. 쉽게 풀어서 수식을 설명하면, 관측 데이터 $x_i$를 중심으로 하고 완만한 정도를 나타내는 $h$(bandwidth)만큼 퍼져있는 kernel function을 생성하고, 이를 모두 더한 다음 샘플의 수 $n$과 $h$를 곱한 값으로 나눠주는 것이다.
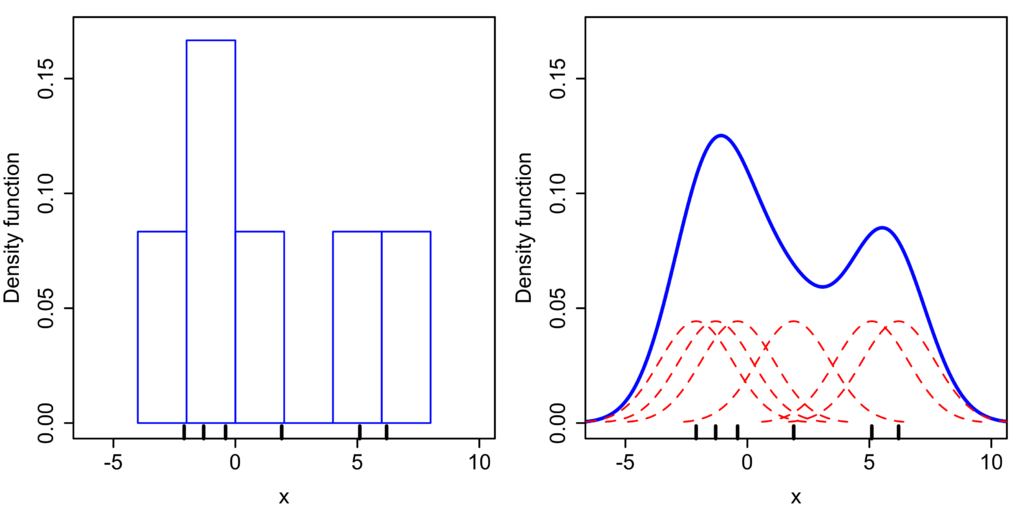
아래의 사진을 보면, 빨간 점선으로 표시된 것이 커널 함수를 통과한 데이터 샘플들이다. 그리고 파란 실선으로 표시된 것이 이를 모두 더한 후 regularization을 한 것이다.
그림에서 알 수 있듯이 이러한 방법은, 히스토그램을 어느정도 스무딩(smoothing)한 것이다.
가장 general 하게 사용될 수 있는 Kernel Density Estimation은 Gaussian Kernel Density Estimation이 있다.
Gaussian Kernel function은 다음과 같다.
- $K(u) = {1\over(2\pi h^2)^{1\over2}} \exp{-{u^2\over2h^2}}$
그리고 Gaussian Kernel Density Estimation은 다음과 같은 수식을 보인다.
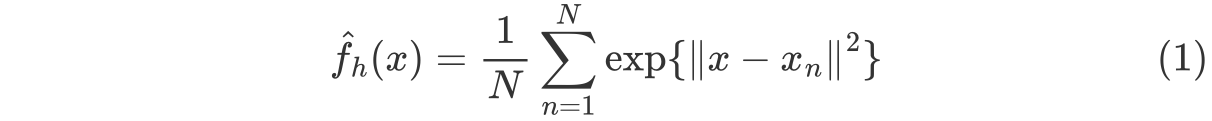
댓글남기기